Nun sind wir also mittendrin in der zweiten Welle oder doch nicht?
Ich behaupte nach wie vor: Die aktuelle „Welle“, also die aktuelle Zunahme der Zahl der Infizierten pro Tag ist eine reine „Testwelle“. Damit nimmt nicht die Zahl der Infizierten zu sondern die Zahl der durch Tests gefundenen Infizierten.
Analyse
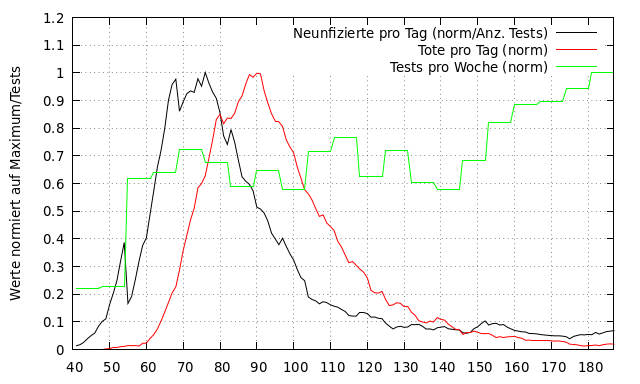
In der folgenden Abbildung ist der Verlauf der Zahl der Neuinfizierten pro Tag (schwarz) normiert auf die Zahl der Tests vergleichend mit dem Verlauf der an Covid-19 Verstorbenen pro Tag (rot) dargestellt. Die gezeigten Werte entsprechen jeweils dem gleitenden Mittel über sieben Tage. Außerdem sind die Zahlen normiert auf das jeweilige Maximum, damit die Kurven besser miteinander vergleichbar sind. Ebenso ist der Verlauf der Tests pro Woche (grün) als normierte Werte dargestellt ohne Berechnung eines gleitenden Mittels.
Man erkennt, dass um Tag 150 die Kurve leicht nach oben geht. Im Vergleich zum Maximum um Tag 70, sind die aktuellen Werte um circa den Faktor 10 kleiner.
Bei einem geringen Anteil positiv Getesteter zur Gesamtzahl aller Getesteten, besteht das Problem der sogenannten „falsch-positiv“ ermittelten. Wie hoch dieser Wert tatsächlich ist, ist zur Zeit nicht genau bekannt. Der Anteil der positiv Getesteten zur Gesamtzahl der durchgeführten Tests liegt seit Tag 125 um oder unter 1 Prozent.
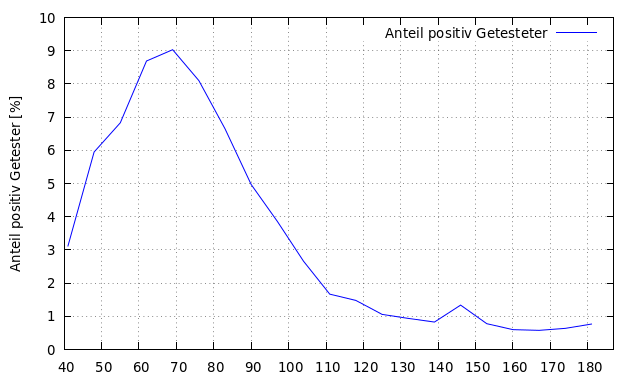
Aktuell fallen nur noch 0,6% aller Tests positiv aus (für KW27-29) und 0,8% für KW30.
Die Bevölkerung ist verunsichert. Wer versteht schon genau, was die Zahlen besagen? Es wäre doch wünschenswert, etwas Unsicherheit zu entfernen. Zum Beispiel, in dem man den Wert der falsch-positiven Testergebnisse ermittelt. Im Folgenden formuliere ich daher Hypothesen, mit denen wir recht einfach prüfen könnten, wie viele, der aktuell als infiziert detektierten Menschen, tatsächlich infiziert sind.
Hypothese 1:
Alle aktuell positiv Getesteten sind falsch-positiv getestet.
Um diese Hypothese zu prüfen, müssten alle in einer Woche positiv Getesteten erneut getestet werden. Sollte es sich bei den aktuell positiv Getesteten tatsächlich um falsch positive Ergebnisse handeln, müsste als Ergebnis wieder ein Bruchteil als infiziert festgestellt werden.
Beispielrechnung: In einer Woche werden 500.000 Tests durchgeführt. Von diesen werden 5.000 als infiziert ermittelt. Das entspricht 1 %. Handelt es sich bei diesen 5.000 um falsch-positiv ermittelte und werden diese erneut getestet, müsste man 50 Infizierte feststellen.
Hypothese 2:
Alle aktuell positiv Getesteten sind richtig-positiv getestet.
Um diese Hypothese zu prüfen, müssten alle in einer Woche positiv Getesteten erneut getestet werden. Sollte es sich bei den aktuell positiv Getesteten tatsächlich um richtig positive Ergebnisse handeln, müsste als Ergebnis nahezu 100% Infizierte festgestellt werden.
Beispielrechnung: In einer Woche werden 500.000 Tests durchgeführt. Von diesen werden 5.000 als infiziert ermittelt. Das entspricht 1 %. Handelt es sich bei diesen 5.000 um richtig-positiv ermittelte und werden diese erneut getestet, müsste man 5.000 Infizierte feststellen.
Interpretation
Der Unterschied zwischen den zu erwartenden Zahlen ist groß. Wenn weniger als 100 Infizierte ermittelt werden, stimmt Hypothese 1. Sollten tatsächlich 4.900 oder mehr Infizierte festgestellt werden, stimmt Hypothese 2. Liegt der Wert irgendwo dazwischen, können wir auf die Qualität der Tests zurückshcließen und den tatsächlichen „falsch-positiv“ Anteil ermitteln.
Beispiel: Es werden 500.000 Tests durchgeführt. 5.000, also 1 %, werden als infiziert ermittelt. Im zweiten Test dieser 5.000 werden noch 2.500 als infiziert ermittelt. Dann war die Hälfte der ersten Testreihe falsch-positiv, also die Hälfte von 1 %, was einer Fehlerquote von 0,5 % entspricht.
Anstatt die Zahl der Tests nun immer weiter zu erhöhen, sollte man besser die positiv Getesteten erneut testen.
Das wäre doch mal ein netter Versuch: Herr Streeck – wie wär’s?