Wie schon bei der ersten Welle zu beobachten war, scheint sich auch dieses mal das Infektionsgeschehen bereits vor Inkrafttreten des Lockdowns zum Besseren hin zu wenden. Der erste Lockdown trat zum 23.03.2020, der zweite zum 02.11.2020 in Kraft.
Bewertung an Hand des R-Faktors
Während der ersten Welle war dies sehr deutlich am Verlauf des R-Faktors zu erkennen. Bereits 20 Tage vor Inkrafttreten des Lockdowns hatte der R-Wert sein Maximum von 10,6 erreicht. Bis zum Start des Lockdowns war dieser Wert auf weniger als 20 % des Maximums abgefallen. Der zweite Lockdown trat zum 02.11.2020 (t_{286}) in Kraft. Die geplanten Maßnahmen sollen vor allem eines bewirken: Ein Verlangsamung der Zunahme und schließlich ein Rückgang der täglichen Neuinfektionen. Dies kann auch für die zweite Welle am Verlauf des R-Faktors untersucht werden. Die folgende Abbildung zeigt, dass das Maximum am 29.10.2020 (t_{282}) erreicht ist und seit dem stetig fällt. Der R- Wert beginnt somit seine fallende Tendenz bereits vier Tage vor Beginn des Lockdowns.
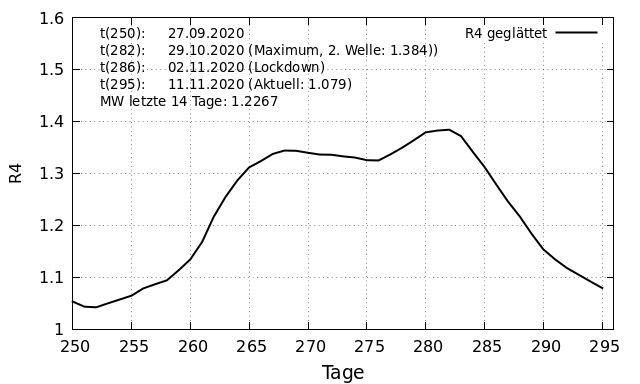
Bewertung an Hand des Kurvenverlaufs
Als weiteres Kriterium kann man den Charakter des Kurvenverlaufs betrachten. Ein dauerhaft exponentielles Wachstum wäre möglicherweise kritisch. Betrachten wir zunächst den Verlauf der ersten Welle. Die folgende Abbildung zeigt, dass die Originaldaten nicht mit einer Exponentialfunktion sondern mit einer sigmoidalen Funktion korrekt beschrieben werden. Der charakteristische Wendepunkt wurde zum 20.03.2020 und damit 3 Tage vor dem ersten Lockdown ermittelt.
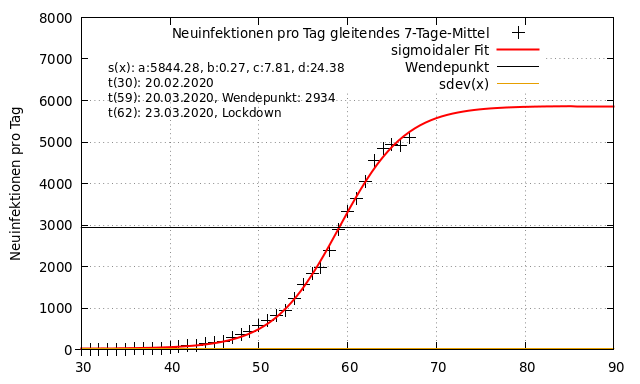
Die Frage zur zweiten Welle lautet: Bleibt der exponentielle Charakter, der zu Beginn der zweiten Welle zu beobachten war, erhalten oder geht auch dieser in einen sigmoidalen Verlauf über, wie in der ersten Welle? Diese Frage kann klar beantwortet werden. Der exponentielle Verlauf ist vorüber. Bis zum 07.11.2020 lässt sich der Verlauf der Zahl an Neuinfektionen pro Tag deutlich besser mit einer sigmoidalen Kurve beschreiben, wie auf der folgenden Abbildung zu erkennen ist. Ein sigmoidaler Verlauf bedeutet, dass eine exponentielle Phase zunächst in eine lineare Entwicklung und dann in eine Sättigungsphase übergeht. Das bedeutet zunächst einmal ganz einfach, das exponentielle Wachstum ist beendet.
Ein sigmoidaler Verlauf ist durch einen Wendepunkt charakterisiert, an dem sich die Entwicklung umkehrt und sich die Zunahme verlangsamt. Dieser Wendepunkt bestimmt sich zu t_{276} (23.10.2020) und liegt 10 Tage vor dem Beginn des Lockdowns, der an t_{286} (02.11.2020) in Kraft trat. Wie schon für R-Faktor beschrieben, ist eine Verbesserung vor dem Lockdown festzustellen.
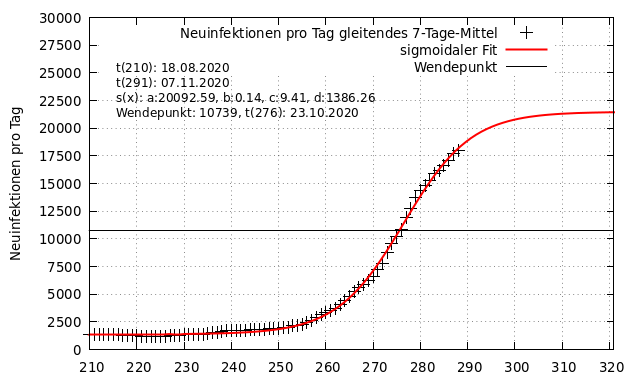
Bestimmung Maximum der 2. Welle
Um eine Prognose abgeben zu können, wann das Maximum der zweiten Welle eintreten könnte, betrachte ich zunächst den Verlauf der ersten Welle. Ein wellenförmiger Verlauf lässt sich weder mit einer Exponentialfunktion noch mit einer sigmoidalen Funktion beschreiben. Deshalb kommt an dieser Stelle die Gaußsche Glockenkurve zum Einsatz. Die Grundformel der Gaußschen Glockenkurve sieht recht simpel aus:
g(x)=e^{-x^{2}}Diese Funktion muss parametrisiert werden, um Amplitude, Breite, Grundlinie und Zeitpunkt der Kurve korrekt abzubilden. Außerdem ist zu beachten, dass der Abfall der ersten Welle langsamer erfolgt als der Anstieg. Dazu wird ein „Asymmetrie“-Faktor (asym) eingeführt. Die parametrisierte Formel sieht wie folgt aus:
g(x) = A*e^{-((x+B)*(C*(1-asym*x)))^{2}}+DDabei bestimmt A die Amplitude, das Maximum, -B verschiebt in positive X-Richtung, C bestimmt die Breite und (1-asym*x) sorgt dafür, dass der abfallende Teil flacher erfolgt. Letzteres gilt nur für einen bestimmten Wertebereich von x um das Maximum. D verschiebt die Kurve in positive Y-Richtung.
Die folgende Abbildung zeigt den Verlauf der über ein 7-Tage Mittel geglätteten Originaldaten (schwarze Symbole) sowie zwei Gaußsche Glockenkurven. Die rote, gestrichelte Kurve zeigt die symmetrische Glockenkurve, die durchgezogene rote Linie die asymmetrische. Letztere beschreibt den Verlauf der Originaldaten auch bezüglich der abfallenden Flanke gut. Die symmetrische Kurve beschreibt die ansteigende Flanke und das Maximum treffend und weicht nur bei der fallenden Flanke ab. Das Maximum wird zu t_{70} (31.03.2020) ermittelt. Wichtig ist, dass gezeigt werden kann, dass auch eine symmetrische Glockenkurve zu einer korrekten Berechnung des Maximums führt.
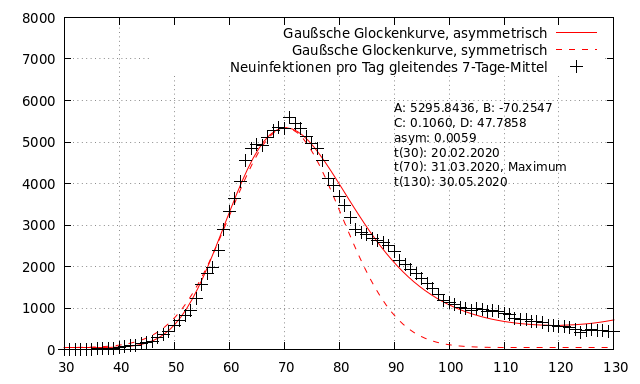
Die gleichen Funktionen werden nun auf die zweite Welle angewendet unter Anpassung der Parameter. In der folgenden Abbildung wird aber nur die asymmetrische Glockenkurve als rote durchgezogene Linie zusammen mit den geglätteten Originaldaten (schwarze Punkte) dargestellt. Der Verlauf der täglichen Zahl an Neuinfektionen wird durch die Kurvenfunktion gut beschrieben. Die Kurve hat im Vergleich zu ersten Welle ein größeres Maximum, Anstieg und Abfall erfolgen etwas flacher, wodurch die Glocke etwas breiter wird. Das Maximum wird an t_{293} (09.11.2020) beobachtet. Dies ist bezogen auf den Stand der Veröffentlichung vor drei Tagen. Ich möchte daher an dieser Stelle noch einmal darauf hinweisen, dass das gleitende Mittel so berechnet wird, dass der letzte vorhandene Datenpunkt 3 Tage vor den täglichen Daten liegt: t_{x} ist der vierte Tage des 7-Tage Intervalls, das gemittelt wird und liegt damit in der Mitte der zu mittelnden Intervalls.
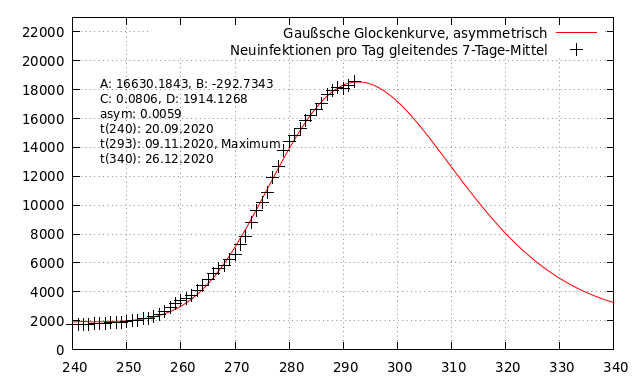
Sollten erste und zweite Welle ähnlichen Mechanismen unterliegen, erscheint die Annahme, dass auch der Kurvenverlauf der zweiten Welle durch die Gaußsche Glockenfunktion angenähert werden kann, plausibel. Das Maximum der zweiten Welle müsste somit heute oder spätestens morgen erreicht sein.
Prognose auf Basis der Glockenkurve
Wie schon in anderen Darstellungen, überlagere ich die Gaußsche Glockenfunktion mit einer Sinusfunktion, um die wöchentlichen Schwankungen der nicht-geglätteten Werte berücksichtigen zu können. Die Überlagerung erfolgt so, dass sich die Amplitude des Sinus proportional zur Glockenfunktion verändert. Die Funktion sieht etwas vereinfachend dargestellt wie folgt aus, wobei die Gaußsche Glockenfunktion nur als g(x) dargestellt ist. g(x) entspricht der oben gegebenen parametrisierten Funktion.
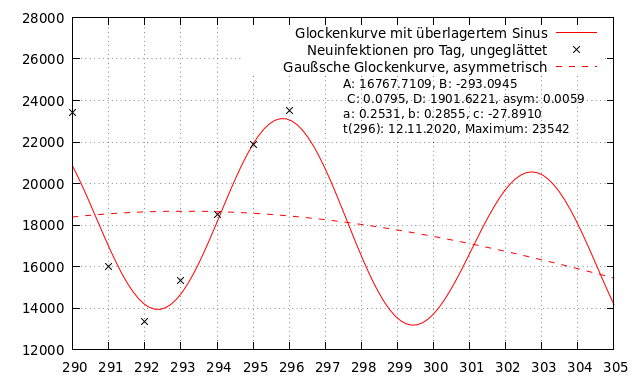
f(x) = a * g(x) * sin(b * pi * (x+c)) + g(x)Die folgende Abbildung zeigt diese Funktion als durchgezogene rote Linie zusammen mit den schwarz dargestellten Originaldaten zur täglichen Zahl an Neuinfizierten. Die rote, gestrichelte Linie zeigt die Gaußsche Glockenfunktion. Es handelt sich hierbei um die gleiche Funktion, wie in der vorigen Abbildung.
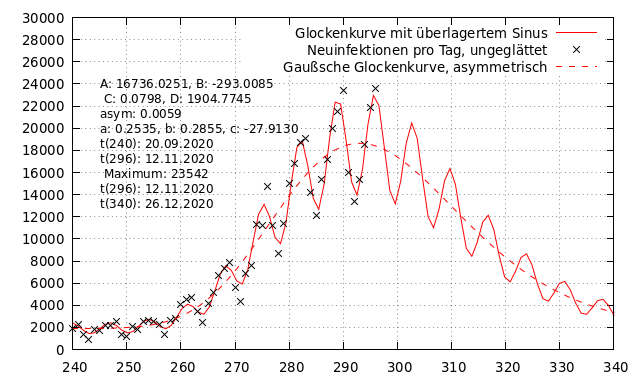
Aus dieser Kurve lässt sich die tägliche Zahl an Neuinfizierten für die kommenden Tage angeben. Für die nächsten fünf Tage prognostiziere ich die folgenden Werte. Wie immer werde ich Daten nutzen, um die Entwicklung der realen zahlen bewerten zu können: Sind die realen Werte niedriger als die Prognosewerte, wird die Situation besser als erwartet.
| 13.11. | 14.11. | 15.11. | 16.11. | 17.11. |
| 20.500 | 16.500 | 13.500 | 13.500 | 16.500 |
Ich habe die Werte in der Tabelle korrigiert, um Tipp- beziehungsweise Ablesefehler zu korrigieren. Im Anschluss findet sich eine Abbildung, die einen kleineren Bereich um das Maximum zeigt, wodurch die Zahlen für die Approximation besser abgelesen werden können. Die Abbildung zeigt den Stand zu t_{296} (12.11.2020).