Auf dieser und folgenden Seiten wird dem Geheimnis des Reproduktionsfaktors auf die Spur gegangen. Immer wieder berichtet das RKI einen Reproduktionsfaktor größer als 1. Das RKI merkt an, dass man mit der Bewertung dieses Wertes vorsichtig sein soll, da der Wert fehlerbehaftet sei. Die Erhöhung über 1 scheint nicht lange anzuhalten, oft nur für einen Tag. Wie kritisch ist diese sporadische, fehlerbehaftete Erhöhung zu sehen? Deutet diese einen Trend an und wenn ja, welchen?
Aus meiner Sicht genügt es nicht, einen Einzelwert zu nennen. Dahinter gehört eine tiefer gehende Auswertung und Erklärung. Auf dieser und noch zu erstellenden Seiten versuche ich genau dies zu tun.
Fangen wir von vorne an: bei den Infektionszahlen, wie sie vom RKI publiziert werden. Die folgende Abbildung zeigt die Zahl der Neuinfektionen pro Tag ab dem 20.02.2020 (t_{30}). Man erkennt deutlich, dass die Werte nicht kontinuierlich zu- und abnehmen sondern von Berg zu Berg schwanken.
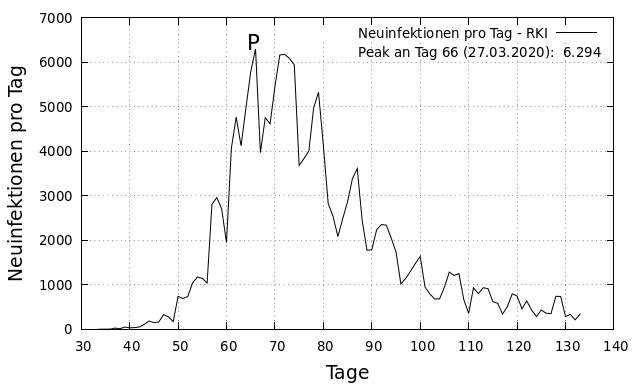
Im nächsten Schritt soll der Verlauf der Zahl der Neuinfektionen pro Tag mathematisch etwas genauer unter die Lupe genommen werden. Man kann an den Originaldaten erkennen, dass diese vom Peak (P: 6.294, t_{66}: 27.03.2020) an exponentiell abfallen und dies oszillierend. Die Amplitude der Schwingungen nimmt dabei mit zunehmender Dauer ab. Stimmt diese Beschreibung, kann man eine abnehmende Exponentialfunktion mit einer Funktion, die eine gedämpfte Schwingung beschreibt, überlagern:
f(x) = Ae * e^{\frac{x + Ce}{\tau_{e}}} + As * e^{\frac{x}{\tau_{s}}} * sin(Bs * pi * (x + Cs))Der erste Teil der Funktion (alles vor dem +) ist die Exponentialfunktion, die den Abfall der Werte beschreibt. Nach dem Pluszeichen folgt eine weitere Exponentialfunktion, die als Koeffizient für die folgende Sinusschwingung dient. Da es sich bei dieser Exponentialfunktion auch um eine fallende Exponentialfunktion handelt und die Y-Werte mit der Zeit immer kleiner werden, wird aus der Sinusschwingung eine gedämpfte Sinusschwingung.
Die folgende Abbildung zeigt die obige Funktion zusammen mit den Originaldaten der Neuinfektionen sowie die Einzelfunktionen. Man erkennt, dass die zusammengesetzte Funktion die realen Daten sehr gut beschreibt.
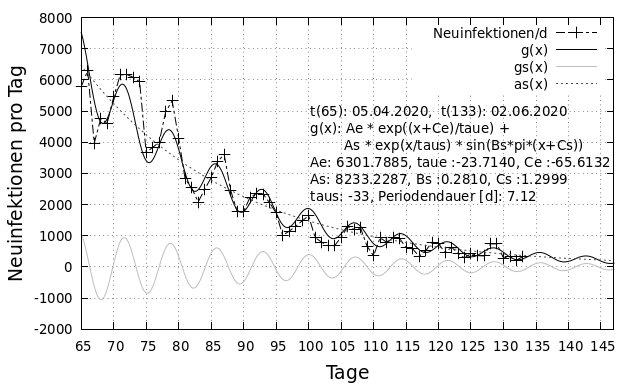
Die schwarze, gestrichelte Linie mit Pluszeichen zeigt die Originaldaten, die schwarze, durchgezogenen Linie die aus Exponentialfunktionen und Sinusfunktion zusammengesetzte Kurve. Die dunkelgrau, gestrichelte Linie zeigt die erste Exponentialfunktion. Die hellgrau, durchgezogene Linie zeigt die gedämpfte Oszillation. Die Summe der beiden grauen Kurven ergibt die durchgezogene, schwarze Kurve.
Ausblick
Im nächsten Beitrag werden die oben beschrieben Zahlen bewertet und die Verteilung Infiziertenzahlen auf Wochentage untersucht. Danach wird der Reproduktionsfaktor genauer betrachtet, der sich aus den oben genannten Daten berechnet.