In Teil 1 wurden die Rohdaten vorgestellt und gezeigt, dass die Zahl der Neuinfektionen nach Erreichen des Peakwertes exponentiell abfallen, überlagert von einer gedämpften Oszillation.
In Teil 2 konnte gezeigt werden, dass die Werte genau im Wochenrhythmus schwanken, mit dem höchsten Wert am Donnerstag und dem niedrigsten Wert am Sonntag. Außerdem konnte gezeigt werden, dass bei konstanter wöchentlicher Zunahme der Zahl der Infizierten, was theoretisch einem Reproduktionsfaktor von 1 entspricht, und als Folge der Schwankungen innerhalb einer Woche, ein Reproduktionsfaktor zwischen 0,71 und 1,49 berechnet wird.
Zusammenfassend bedeutet das, dass bis zu einem R-Wert von fast 1,5, nicht auf eine gefährliche, da exponentielle, Zunahme der Infiziertenzahl gerechnet werden muss.
In diesem Teil 3 geht es darum zu prüfen, ob es Analysemethoden gibt, die weniger störanfällig gegenüber periodischen Abweichungen bezüglich der Zahl der Neuinfektionen sind. Dies wird an denselben, künstlich erzeugten Infiziertenzahlen untersucht, wie in Teil 2 vorgestellt. Beobachtet man periodische Schwankungen, kann man ein so genanntes gleitendes Mittel über die Ausgangsdaten berechnen. Zum Beispiel kann man die Summe der Werte der Zahl an Neuinfektionen von sieben aufeinanderfolgenden Tagen berechnen und durch sieben teilen. Dies erfolgt für jeden Tag. Da man zunächst einmal sieben Tage braucht, um ein sieben-Tage Mittel zu berechnen, startet man an Tag sieben mit der Berechnung für die Tage 1-7. An Tag 8 berechnet man den Mittelwert für die Tage 2-8 und so weiter. Dieses gleitende Mittel kann man auch über 8, 9, 10 oder mehr Tage berechnen, besser ist jedoch eine Dauer, die der Periodendauer in den Ursprungsdaten zumindest möglichst nahe kommt. In vorgestellten Fall wurde eine Periodendauer von 7,12 Tagen für die realen Werte berechnet. Für die künstlich zusammengestellten Infiziertenzahlen ergibt sich eine Periodendauer von genau 7 Tagen.
Die folgende Abbildung zeigt Werte für den Reproduktionsfaktor (R4) für gleitende Mittel berechnet über 7, 8, 9, 10, 11, 12 und 13 Tage.
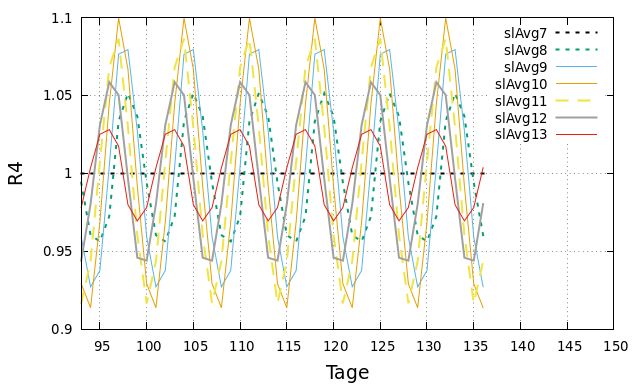
Beinahe unscheinbar aber umso wichtiger in der obigen Abbildung ist die gestrichelte schwarze Linie. Sie zeigt den über ein gleitendes Mittel von sieben Tagen berechneten Reproduktionsfaktor zu den künstliche erstellen Infiziertenzahlen und dieser liegt genau bei 1!
Für reale Daten wird die Periodendauer nicht genau sieben Tagen entsprechen. Durch Feiertage verkürzt sich die vorangegangene Periode und verlängert sich die folgende. Es können aber noch andere Störungen hinzukommen wie technische Probleme bei der Übermittlung sowohl auf der sendenden wie auf der empfangenden Seite. Durch die von mir durchgeführte Analyse über den Zeitraum vom 22.01.2020 bis 02.06.2020 wurde eine Periodendauer von 7,12 Tagen berechnet. Ich habe daher untersucht, wie sich der Reproduktionsfaktor berechnet, wenn man das gleitende Mittel nicht nur über sieben Tage berechnet. Die obige Abbildung zeigt, dass bei einem gleitenden Mittel berechnet über sieben Tage sich die Schwankungen genau aufheben und ein konstanter Wert von 1 für den Reproduktionsfaktor ermittelt wird. Je stärker nun die Dauer, über die das gleitenden Mittel berechnet wurde von der tatsächlichen Periodendauer abweicht, um so größer werden die Schwankungen. Für ein gleitendes Mittel über acht Tage sind die Schwankungen am kleinsten und für ein gleitendes Mittel über zehn Tage am größten.
Zusammenfassend kann man sagen, dass eine gleitende Mittelwertberechnung, die über eine Periode mittelt, die der Dauer der Schwingungen entspricht, die in den realen Daten gemessen wurde, Schwankungen um einen konstanten Mittelwert und daraus resultierende Störungen des resultierenden Reproduktionsfaktors sehr gut ausgleichen kann.
Ausblick
In Teil 4 werden die in den Teilen 1-3 vorgestellten Ergebnisse zusammengefasst und Vorschläge unterbreitet, wie wir als Gesellschaft mit der Pandemie zukünftig umgehen könnten.