Entwicklung und Prognose der Zahl der Neuinfektion pro Tag, zweite Welle
Am 10.06.2020 hatte ich mit Prognosen über die Entwicklung der Zahl der Neuinfektionen pro Tag begonnen. Ich nannte die Prognose „Wetter“-Prognose, da die Vorhersage nur für wenige Tage gelten sollte. Heute greife ich die Idee wieder auf und möchte betonen, dass die Prognosen nicht den Anspruch haben, den tatsächlichen Verlauf vorherzusagen. Die Prognosen gehen von folgenden Annahmen aus:
- Die aktuelle Entwicklung basiert auf dem Zusammenspiel bestimmter und entscheidender Faktoren
- Es ist unwichtig, um welche Faktoren es sich handelt und welche Werte diese annehmen
- Die relevanten Faktoren sind stabil, wirken also unverändert
- Unter dieser Annahme wird eine Funktion entwickelt, die ausreichend genau den Verlauf der realen Daten beschreibt
Daraus leite ich folgende Punkte ab:
- Eine deutliche und über mehrere Tage andauernde Abweichung der realen Daten von den vorhergesagten Daten gibt einen Hinweis darauf, dass sich an den „entscheidenden Faktoren“ etwas geändert hat
- Diese Änderung kann sowohl eine Verschlechterung oder eben auch eine Verbesserung darstellen
- Die Richtung der Abweichung der realen Daten von der Prognose erlaubt eine Interpretation, ob es sich um eine Verbesserung oder Verschlechterung handelt
Die folgende Abbildung zeigt den Verlauf der Neuinfektionen pro Tag wie vom RKI publiziert (rote Sterne), sowie das gleitenden Mittel über 7 Tage zu den Neuinfektionen pro Tag (schwarzes +). Die Auswertung beginnt ab t_{210} (18.08.2020). Das gleitende Mittel wird bezogen auf den aktuellen X-Wert aus den drei davor liegenden und den drei danach folgenden Tagen berechnet. Beispiel: Der Wert für Tag 4 wird aus dem Mittelwert der Tage 1-7 bestimmt. An die schwarze Kurve der gleitenden Mittelwerte wurde eine einfache Exponentialfunktion der Form angenähert:
e(x)=A * exp((x+C)/tau) + DZur Beschreibung der Originaldaten musste eine etwas komplexere Funktion herangezogen werden, da die Daten eine Schwankung im Wochenrhythmus aufzeigen. Die Grundtendenz ist in beiden Fällen die gleiche:
f(x)=a1 * exp((x+ce1)/taus) * sin(b1 * pi * (x+c1)) + A3 * exp((x+C3)/tau3) + D3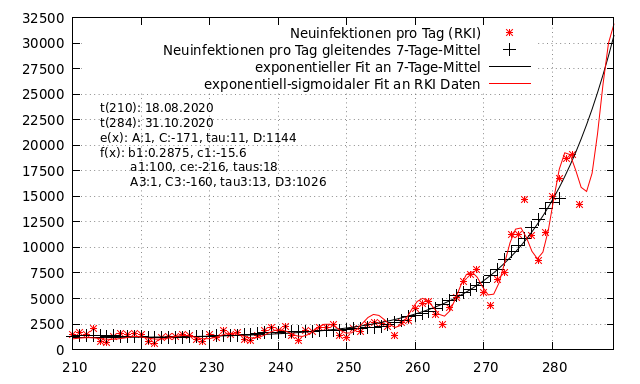
Zum Ablesen der Werte für die nächsten drei Tage zeigt die folgende Abbildung einen zeitlich vergrößerten Ausschnitt der letzten zwei Wochen vor dem aktuellen Datum und der folgenden drei Tage:

Für die nächsten drei Tage ergibt sich daraus für die Zahl der Neuinfektionen pro Tag folgende Vorhersage:
| 01.11. | 02.11. | 03.11 |
| 15.500 | 18.000 | 23.500 |
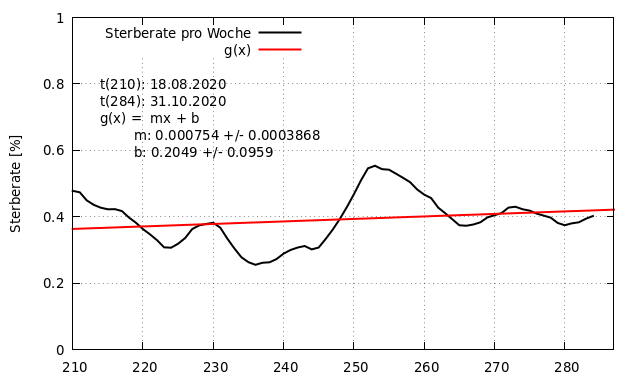
Zusätzlich zur Vorhersage der Entwicklung der Zahl an Neuinfektionen wird noch die Entwicklung der (Fall-) Sterberate betrachtet. Fallsterberate bedeutet in diesem Kontext, dass ausschließlich die vom RKI genannten Zahlen zu Infizierten und Toten zur Berechnung herangezogen werden. Dabei wird das gleitende 7-Tage Mittel zu den vom RKI publizierten Zahlen verwendet und die Sterberate pro Woche berechnet. Es wird dabei nicht berücksichtigt, dass eine bestimmte Zeit von der Infektion bis zum Tod vergeht. Das bedeutet, berechnet man die Fallsterblichkeit in einer Phase, in der die Infektionszahlen stark steigen, wird die Fallsterblichkeit unterschätzt. Berechnet man die Fallsterblichkeit dagegen in einer Phase, in der die Infektionszahlen stark fallen, wird die Fallsterblichkeit überschätzt. Damit hat die so gewonnene Darstellung der Fallsterblichkeit einen Phasenversatz zur tatsächlichen Entwicklung der Fallsterblichkeit. Um so längere Zeiträume für die Berechnung der Fallsterblichkeit herangezogen werden, um so geringer ist der Effekt dieses Phasenversatzes.
Die folgende Abbildung zeigt den Verlauf der Sterberate pro Woche (schwarz) mit einer linearen Approximation. Die Steigung m ist positiv und liegt bei etwa 0,0008 % pro Tag. Die Standardabweichung beträgt etwa +/- 50 %. Die Annäherung ist zwar recht ungenau, trotzdem leite ich die Prognose daraus ab, dass, bei unveränderten Rahmenbedingungen, die Fallsterberate in den nächsten zwei Wochen um 0,01 % zunimmt. Wie für die Entwicklung der Zahl der Neuinfektionen pro Tag lassen sich aus Abweichungen der sich tatsächlich einstellenden Zahlen und der Prognose Veränderungen der Rahmenbedingungen ableiten.